Marco A. García

Social Network Analysis: Exploring Employee Communication through Enron Email Data


Analyzing the structure and dynamics of communication networks within the Enron email dataset to uncover key insights about organizational behavior.


Marco A. García - 26/01/2025

You can find this project in the GitHub repository.

Introduction

The rise of remote work has transformed the way employees communicate, shifting from face-to-face interactions to digital communication channels such as email. Understanding the dynamics of these communication networks is crucial to improving knowledge transfer, identifying key contributors, and analyzing the robustness of these networks.

In this project, we will explore the social network created by email communication within the Enron Corporation, a U.S.-based energy company that ceased operations in 2001. The dataset, derived from the company’s email records, contains information about 143 employees and their email interactions. Specifically:

The goal of this project is to utilize social network analysis techniques to gain insights into the structure, resilience, and centrality of the communication network, as well as to identify the most influential nodes in the network.

Steps to Complete the Project

  1. Load and Explore the Dataset
  1. Construct a Social Network
  1. Analyze the Network
  1. Resilience Analysis
  1. Centrality Measures
  1. Directed Network and PageRank Analysis
  1. Conclusions

Questions to Answer

  1. Network Structure:
  1. Network Resilience:
  1. Centrality Analysis:
  1. Directed Network:

By addressing these questions, we will uncover key insights into the Enron email network, its structure, and the roles played by individual employees in maintaining its connectivity and information flow.

Packages to use

We will use the following Python libraries to analyze and visualize the Enron email network:

  1. NetworkX
    • Create and analyze networks (graphs).
  2. Matplotlib
    • Visualize the network graph.
  3. NumPy
    • Perform numerical operations efficiently.
  4. Pandas
    • Load and manipulate the dataset.
!pip -q install networkx matplotlib numpy pandas
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import numpy as np
import pandas as pd

1. Load and Explore the Dataset

Great, let’s start by downloading our email-enron-only.mtx file and uploading it to our working environment. We’ll use pandas to load it into a DataFrame, which contains two important columns: Sender (the employee sending the email) and Receiver (the employee receiving it). Next, we’ll explore our dataset by printing the first few rows, checking its structure with info(), and ensuring there are no duplicates or missing values. This will set a strong foundation for the analysis we’re about to dive into.

data = pd.read_csv("email-enron-only.mtx", sep=" ", header=None, names=["sender", "receiver"])
print(data.head())
print("\n----\n")
print(data.info())
print("\n----\n")
print(f"Duplicated values: {data.duplicated().sum()}")
   sender  receiver
0      17         1
1      72         1
2       3         2
3      19         2
4      20         2

----

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 623 entries, 0 to 622
Data columns (total 2 columns):
 #   Column    Non-Null Count  Dtype
---  ------    --------------  -----
 0   sender    623 non-null    int64
 1   receiver  623 non-null    int64
dtypes: int64(2)
memory usage: 9.9 KB
None

----

Duplicated values: 0

Perfect, having no issues with our dataset, we can now move on to building and visualizing our network. Using NetworkX, we’ll construct an undirected graph where each node represents an employee, and each edge represents an email interaction. Once the graph is created, we’ll visualize it using Matplotlib, customizing the size and color of nodes and edges for clarity.

G = nx.from_pandas_edgelist(data, source="sender", target="receiver")

print(G)
Graph with 143 nodes and 623 edges
def draw_graph(G, title):
  fig = plt.subplots(figsize=(15, 10))
  pos = nx.spring_layout(G)
  nx.draw_networkx_nodes(G, pos=pos, node_size=100)
  nx.draw_networkx_edges(G, pos=pos, alpha=0.3)
  nx.draw_networkx_labels(G, pos=pos, font_size=10)
  plt.title(title)
  plt.show()
draw_graph(G, "Undirected Network of Email Interactions")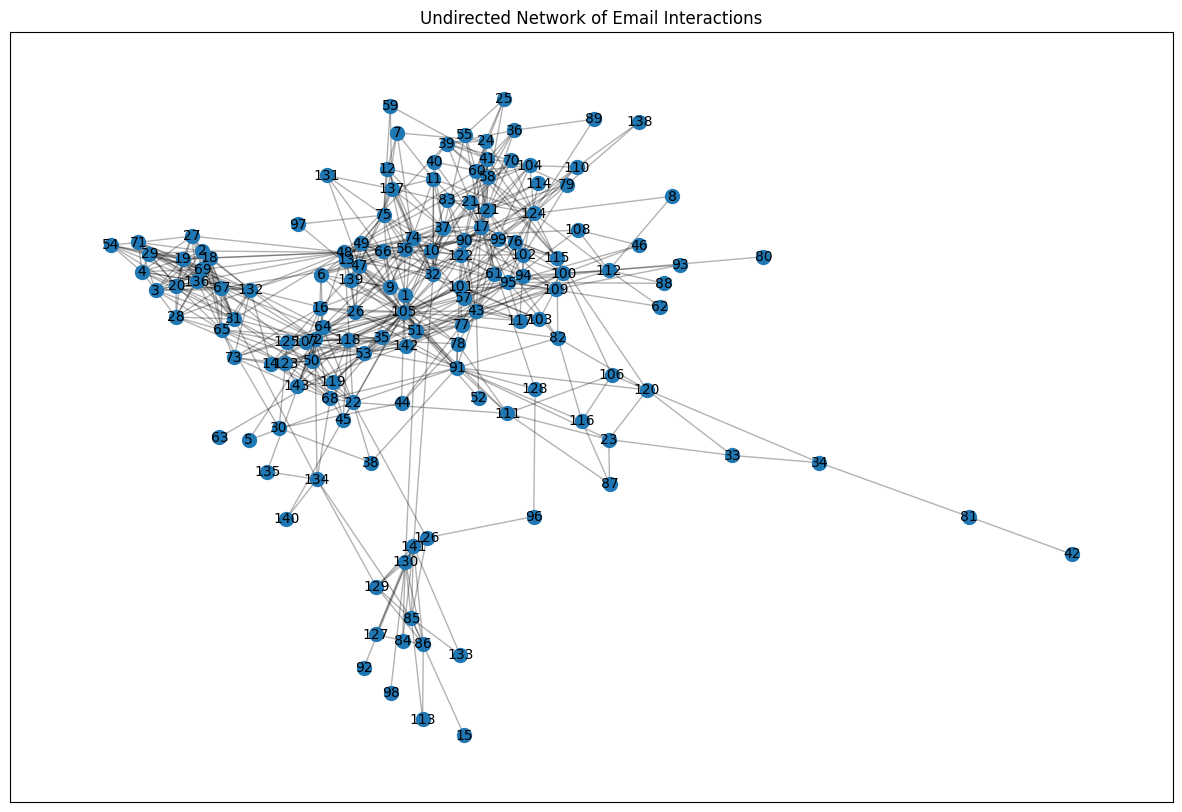

From the graph, we can observe:

3. Analyze the Network {#3-analyze-the-network}

With our network visualized, we will now perform an analysis to uncover key properties and structural insights. This step helps us understand the connectivity and overall behavior of the network.

Goals:

def sort_nodes_by_degree(G, reverse=True):
  return sorted([item for item in G.degree()], key=lambda x: x[1], reverse=reverse)

def get_maxium_degree_nodes(G):
  nodes = sort_nodes_by_degree(G, True)

  return [node for node in nodes if node[1] == nodes[0][1]]

def get_minium_degree_nodes(G):
    nodes = sort_nodes_by_degree(G, False)

    return [node for node in nodes if node[1] == nodes[0][1]]
print(f"Maxium degree nodes: {get_maxium_degree_nodes(G)}")
print(f"Minium degree nodes: {get_minium_degree_nodes(G)}")
print(f"Graph diameter: {nx.diameter(G)}")
print(f"Average shortest path length: {nx.average_shortest_path_length(G)}")
Maxium degree nodes: [(105, 42)]
Minium degree nodes: [(15, 1), (42, 1), (63, 1), (80, 1), (92, 1), (98, 1)]
Graph diameter: 8
Average shortest path length: 2.967004826159756
def draw_shortest_path_hist(G, title):
  node_lengths = dict(nx.shortest_path_length(G))
  lenghts = sum([list(i.values()) for i in node_lengths.values()], [])
  highest = max(lenghts)
  bins = [-0.5 + i for i in range(highest + 2)]
  plt.hist(lenghts, bins=bins, rwidth=0.8)
  plt.title(title)
  plt.xlabel("Distance")
  plt.ylabel("Count")
  plt.show()
draw_shortest_path_hist(G, "Shortest path")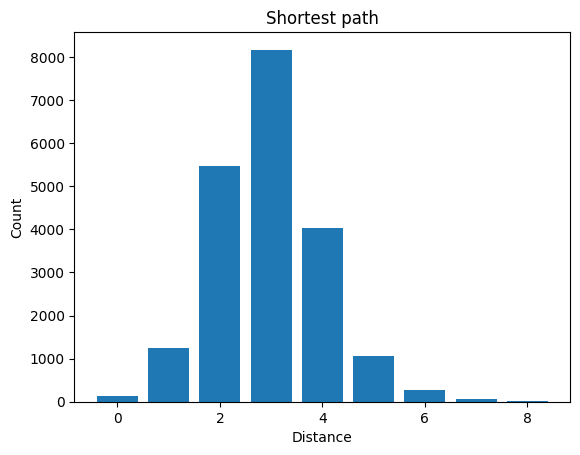

From our analysis of the Enron email network, we can draw the following key insights:

  1. Node with Maximum Degree:
    • The node with the highest degree is 105, with a total of 42 connections.
    • This indicates that node 105 is a central figure in the network, connecting with the largest number of employees and likely playing a critical role in communication.
  2. Nodes with Minimum Degree:
    • The nodes with the lowest degree are 15, 42, 63, 80, 92, and 98, each with only 1 connection.
    • These nodes represent isolated or peripheral employees who are minimally engaged in the network.
  3. Graph Diameter:
    • The diameter of the network is 8, meaning the longest shortest path between any two nodes in the network is 8 steps.
    • This indicates that even in the worst-case scenario, communication can traverse the entire network relatively efficiently within 8 steps.
  4. Average Shortest Path Length:
    • The average shortest path length is approximately 2.97, suggesting that on average, any two nodes are less than three steps apart.
    • This highlights the high connectivity and efficiency of communication within the network.
  5. Distribution of Shortest Paths:
    • The histogram above shows the distribution of shortest paths in the network. Most nodes are connected by paths of length 2 or 3, reinforcing the network’s compactness and its ability to facilitate efficient communication.
  6. Bipartite Network:
    • In this case, the network isn’t bipartite due to the presence of an odd-length cycle. A bipartite network requires that vertices can be divided into two distinct sets where no two vertices within the same set are directly connected.

These metrics provide a foundational understanding of the network’s structure, identifying key contributors, peripheral participants, and the efficiency of message transfer within the email system.

4. Resilience Analysis

Now that we understand the structure of the network, we analyze its resilience (the ability to maintain connectivity when nodes or edges are removed). A resilient network remains functional despite failures or targeted attacks.

def get_random_node(G):
  return [np.random.choice(G.nodes())]
def get_sorted_nodes_by_metric(G, metric, reverse=True):
  nodes = metric(G)

  if isinstance(nodes, dict):
    nodes = [(k, v) for k, v in nodes.items()]

  sorted_nodes = sorted(nodes, key=lambda x: x[1], reverse=reverse)

  return [node[0] for node in sorted_nodes]
def dismantle(G, fn, **args):
  g = G.copy()
  total_nodes = g.number_of_nodes()
  removed_nodes = []
  clusters = []
  nodes_id = []
  n_clusters = []


  while len(g.nodes()) > 1:
    node = fn(g, **args)
    g.remove_node(node[0])
    removed_nodes.append((len(removed_nodes) + 1) / total_nodes)
    nodes_id.append(node[0])
    components = list(nx.connected_components(g))
    g_size = 0
    if len(components) > 0:
      g_size = max([len(c) for c in components]) / total_nodes
    clusters.append(g_size)
    n_clusters.append(len(components))

  return removed_nodes, clusters, nodes_id, n_clusters
def plot_dismantle(x, y, title):
  plt.plot(x, y)
  plt.xlabel("Removed nodes")
  plt.ylabel("Clusters")
  plt.title(title)
  plt.show()
r_removed_nodes, r_clusters, r_nodes_id, r_n_clusters = dismantle(G, get_random_node)
plot_dismantle(r_removed_nodes, r_clusters, "Random")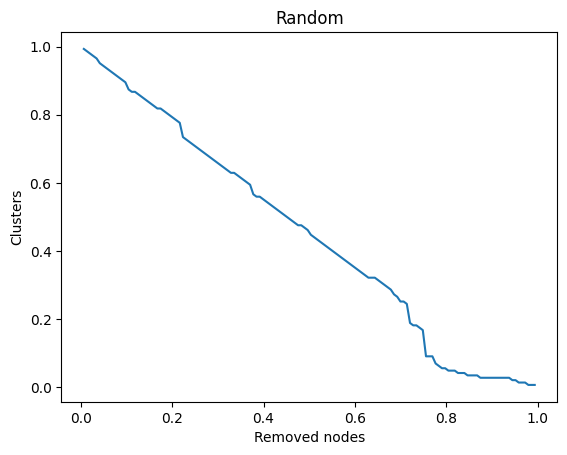

d_removed_nodes, d_clusters, d_nodes_id, d_n_clusters = dismantle(G, get_sorted_nodes_by_metric, metric=nx.degree_centrality)
plot_dismantle(d_removed_nodes, d_clusters, "Degree Centrality")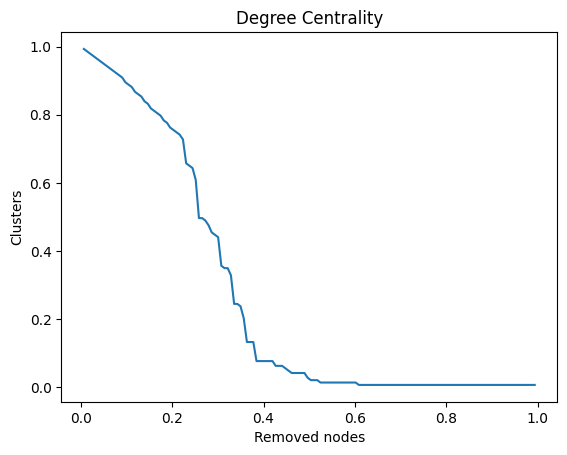

print(f"Articulation points (critical nodes): {list(nx.articulation_points(G))}")
print(f"Bridges (critical edges): {list(nx.bridges(G))}")
Articulation points (critical nodes): [81, 34, 112, 85, 130, 141, 53]
Bridges (critical edges): [(112, 80), (53, 63), (85, 15), (141, 92), (34, 81), (81, 42), (130, 98)]
def critical_nodes_colors(G, critical_nodes):
  node_colors = []

  for node in G.nodes():
    if node in critical_nodes:
      node_colors.append("red")
    else:
      node_colors.append("cyan")

  return node_colors

def critical_edges_colors(G, critical_nodes):
  edge_colors = []

  for edge in G.edges():
    if edge[0] in critical_nodes or edge[1] in critical_nodes:
      edge_colors.append("red")
    else:
      edge_colors.append("black")

  return edge_colors

def draw_critical_graph(G, critical_nodes, title):
  fig = plt.subplots(figsize=(15, 10))
  pos = nx.spring_layout(G)
  nx.draw_networkx_nodes(
      G,
      pos=pos,
      node_size=100,
      node_color=critical_nodes_colors(G, critical_nodes)
  )
  nx.draw_networkx_edges(G, pos=pos, alpha=0.3, edge_color=critical_edges_colors(G, critical_nodes))
  nx.draw_networkx_labels(G, pos=pos, font_size=10)
  plt.title(title)
  plt.axis('off')
  plt.show()
draw_critical_graph(G, list(nx.articulation_points(G)), "Critical Nodes")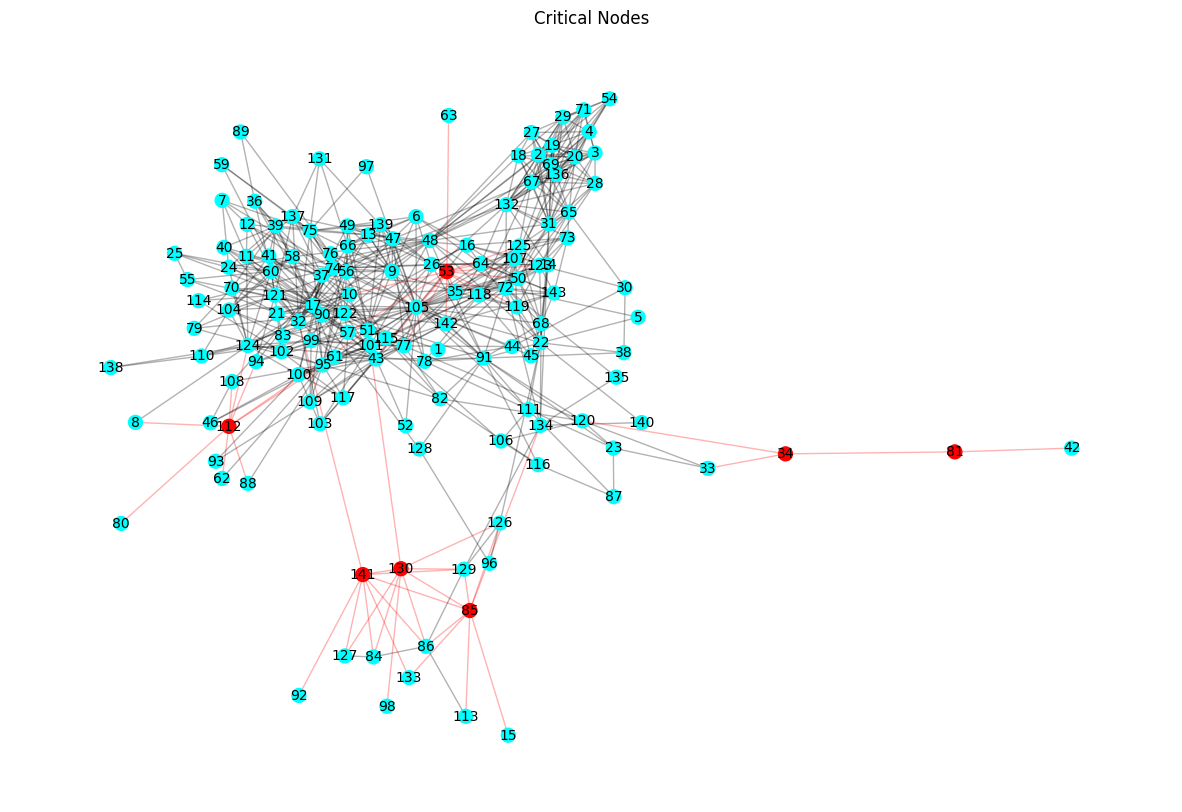

The resilience analysis of the Enron email network reveals the following key findings:

  1. Articulation Points (Critical Nodes):
    • The network contains 7 critical nodes: 81, 34, 112, 85, 130, 141, and 53.\
    • Removing these nodes would fragment the network, indicating their importance in maintaining overall connectivity.
  2. Bridges (Critical Edges):
    • The network has 7 critical edges: (112, 80), (53, 63), (85, 15), (141, 92), (34, 81), (81, 42), and (130, 98).\
    • Removing any of these edges would disconnect specific parts of the graph, making them points of vulnerability.
  3. Network Robustness:
    • According to the graph showing degree centrality-based removal, the network retains acceptable connectivity when 20% to 40% of nodes are removed.\
    • Beyond this threshold, connectivity rapidly declines, but this demonstrates that the network can handle moderate disruptions without complete failure.
  4. Conclusion on Resilience:
    • The network is resistant to random failures or targeted attacks up to a certain extent, maintaining functionality even when key nodes or edges are removed.\
    • However, the presence of articulation points and bridges means that the network is not invulnerable---targeting these components could lead to fragmentation.

5. Centrality Measures

To understand the most influential nodes in the network, we analyze three types of centrality measures: degree centrality, betweenness centrality, and closeness centrality. These measures highlight nodes based on different criteria of importance.

1. Degree Centrality

2. Betweenness Centrality

3. Closeness Centrality

def draw_centrality_graph(G, measures, title):
  plt.figure(figsize=(15, 12))
  pos = nx.spring_layout(G)
  nodes = nx.draw_networkx_nodes(
      G,
      pos,
      node_size=100,
      cmap=plt.cm.plasma,
      node_color=list(measures.values()),
      nodelist=list(measures.keys())
  )
  nx.draw_networkx_edges(G, pos, alpha=0.2)
  nx.draw_networkx_labels(G, pos, font_size=6)
  plt.title(title)
  plt.colorbar(nodes)
  plt.axis('off')
  plt.show()
sorted_degree_centrality = sorted(list(dict(nx.degree_centrality(G)).items()), key=lambda x: x[1], reverse=True)
top_degree_centrality = [node[0] for node in sorted_degree_centrality][:10]
draw_critical_graph(G, top_degree_centrality, "Top 10 Degree Centrality")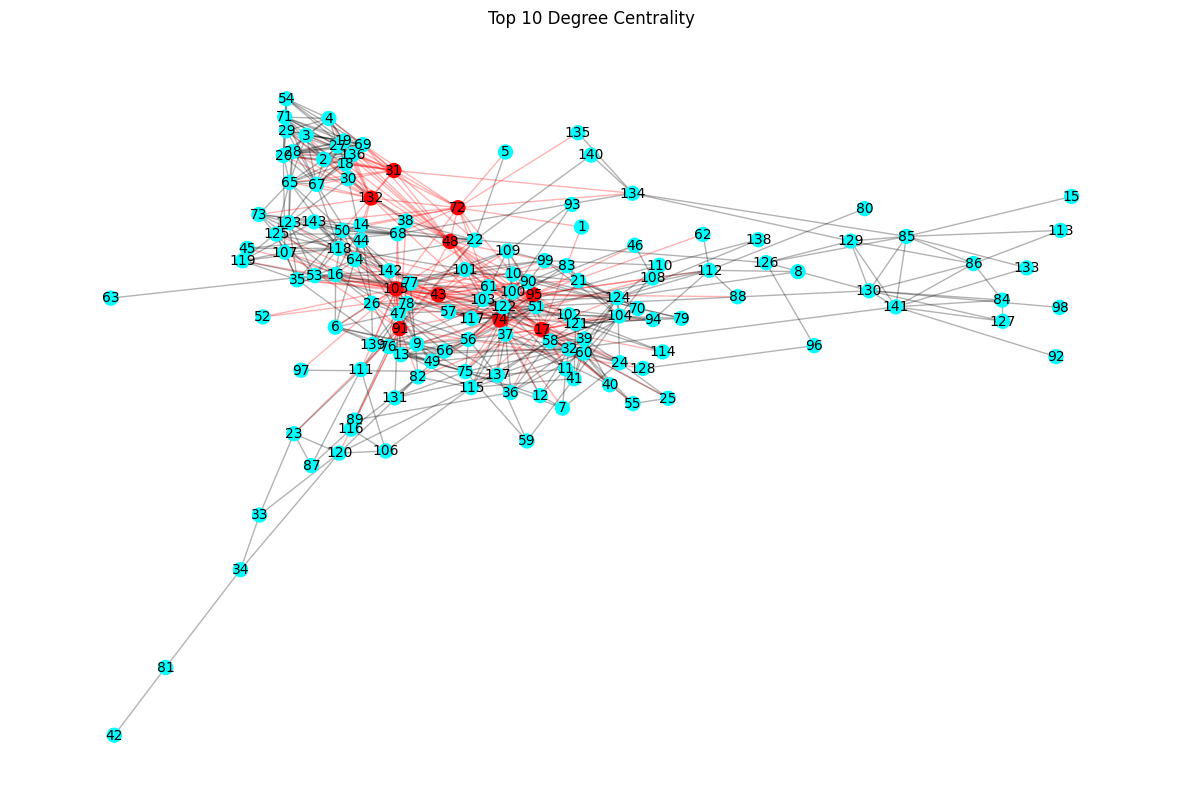

draw_centrality_graph(G, nx.degree_centrality(G), "Degree Centrality")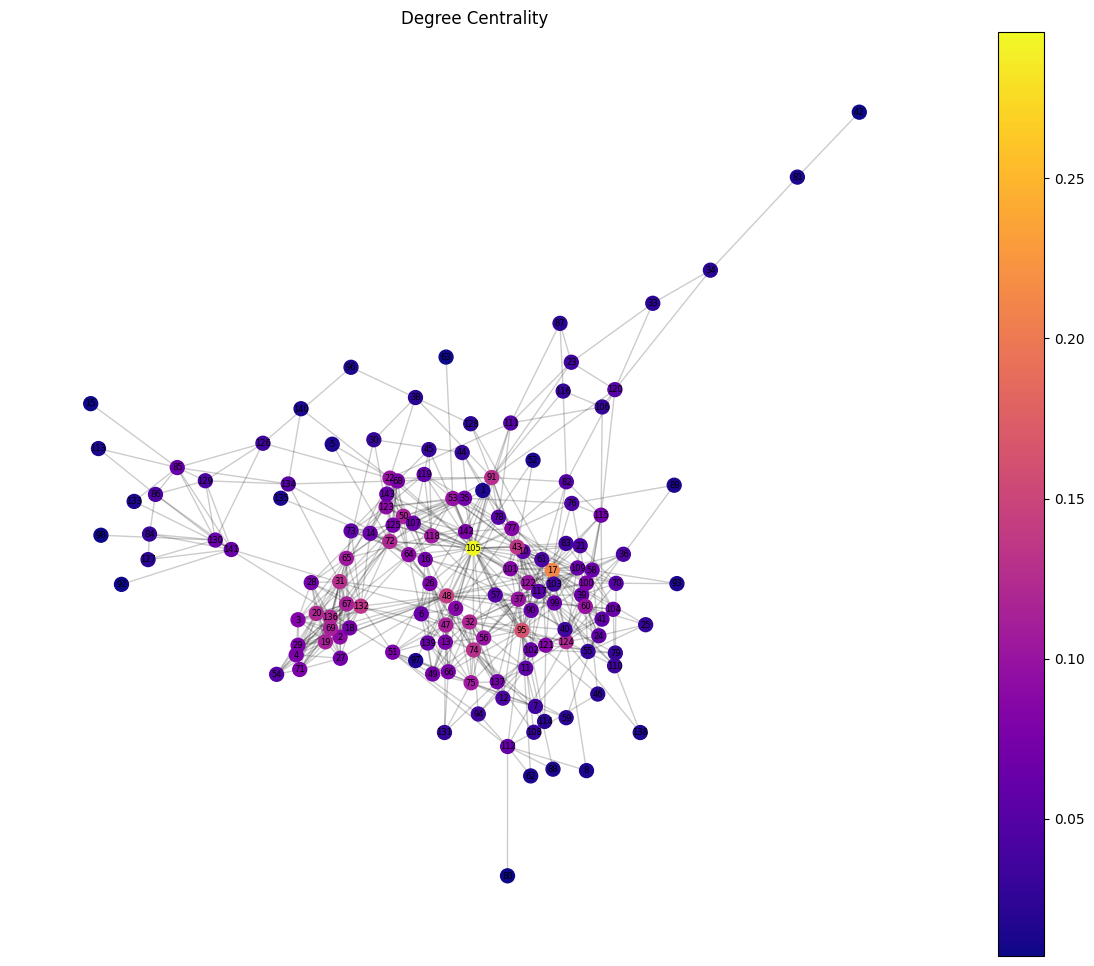

sorted_betweenness_centrality = sorted(list(dict(nx.betweenness_centrality(G)).items()), key=lambda x: x[1], reverse=True)
top_betweenness_centrality = [node[0] for node in sorted_betweenness_centrality][:10]
draw_critical_graph(G, top_betweenness_centrality, "Top 10 Betweenness Centrality")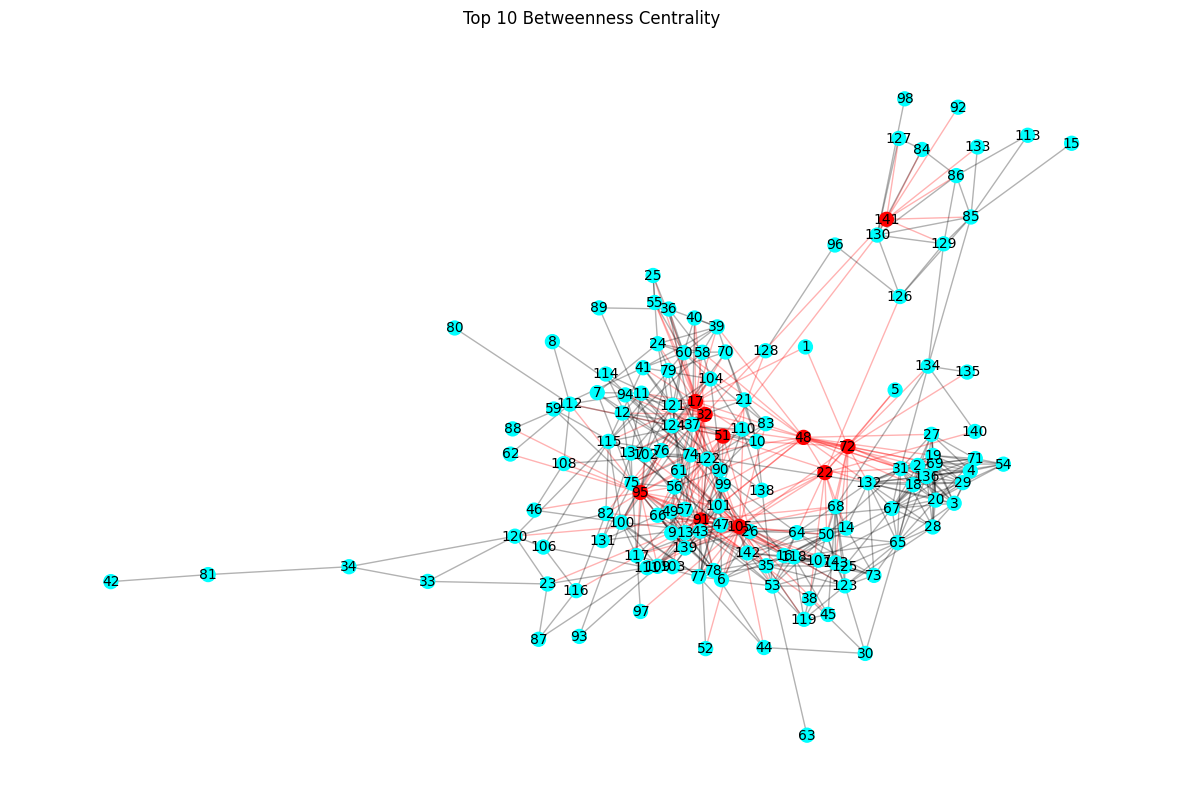

draw_centrality_graph(G, nx.betweenness_centrality(G), "Betweenness Centrality")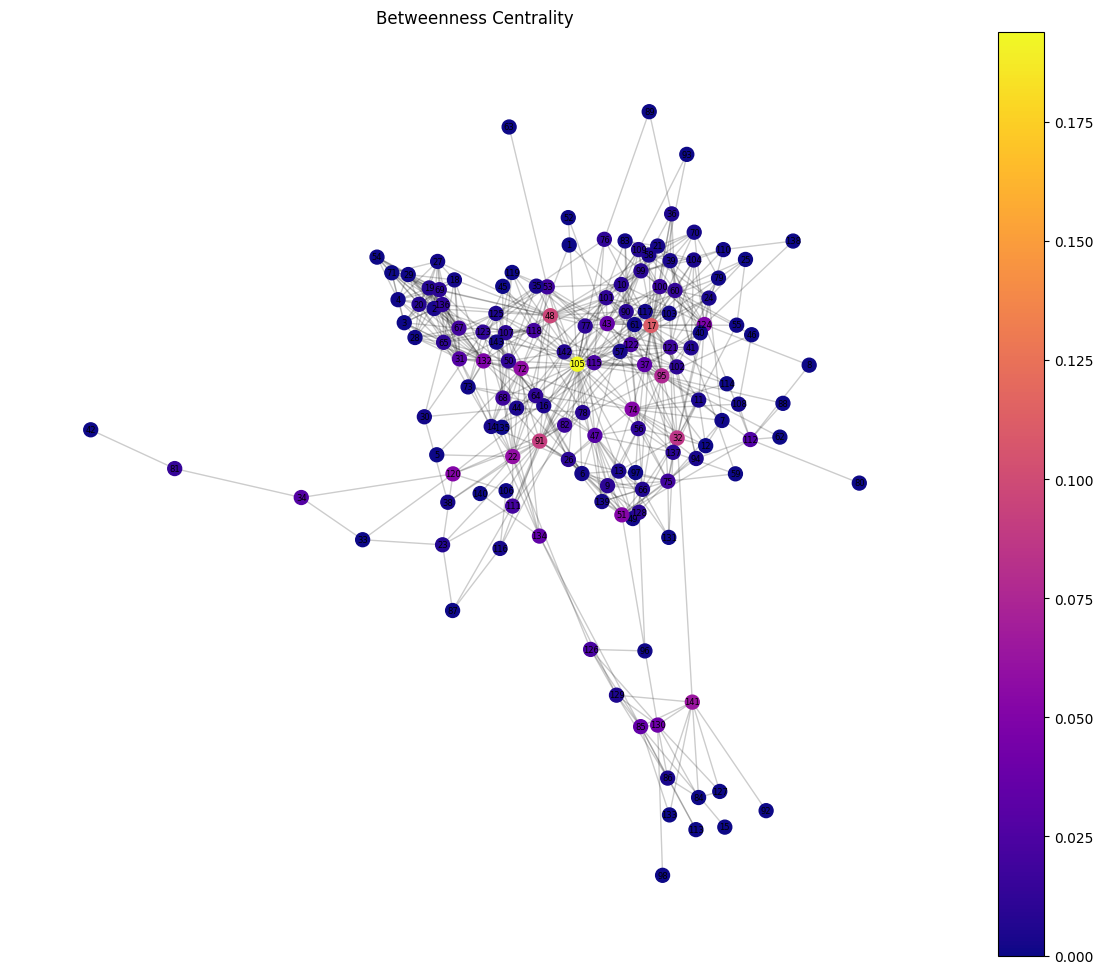

sorted_closeness_centrality = sorted(list(dict(nx.closeness_centrality(G)).items()), key=lambda x: x[1], reverse=True)
top_closeness_centrality = [node[0] for node in sorted_closeness_centrality][:10]
draw_critical_graph(G, top_closeness_centrality, "Top 10 Closeness Centrality")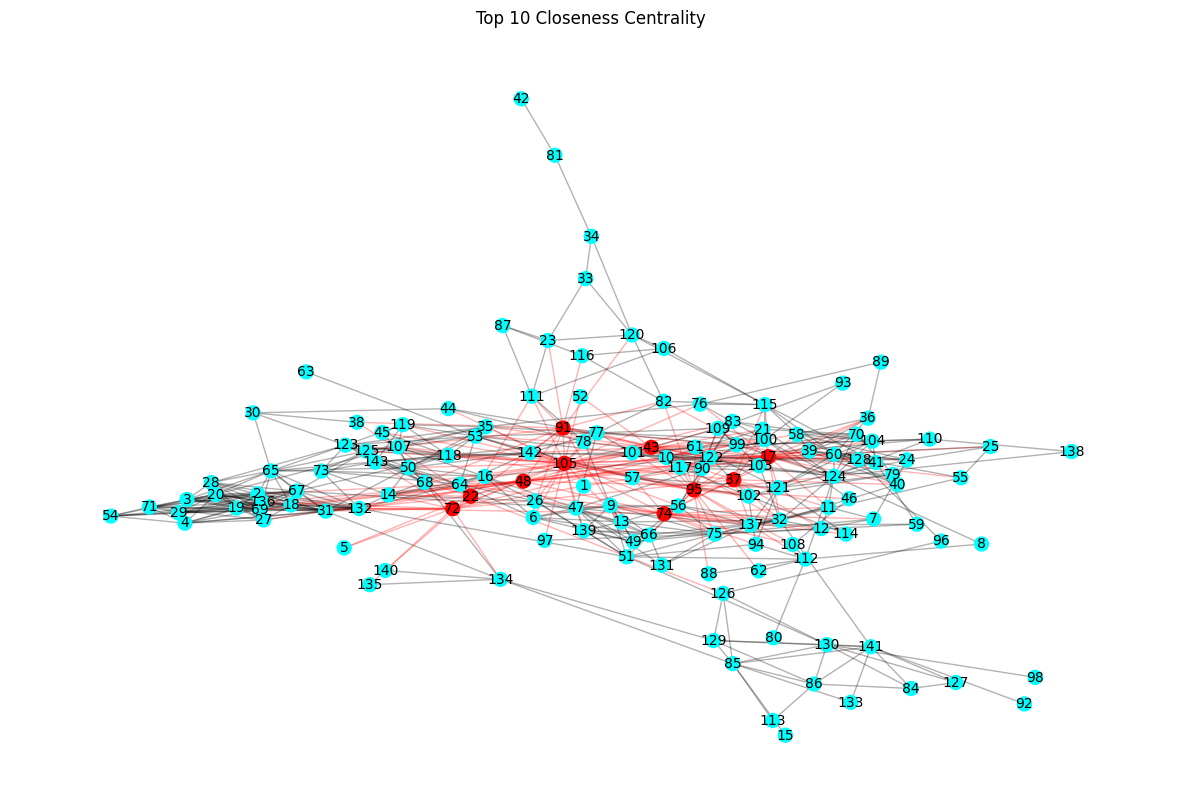

draw_centrality_graph(G, nx.closeness_centrality(G), "Closeness Centrality")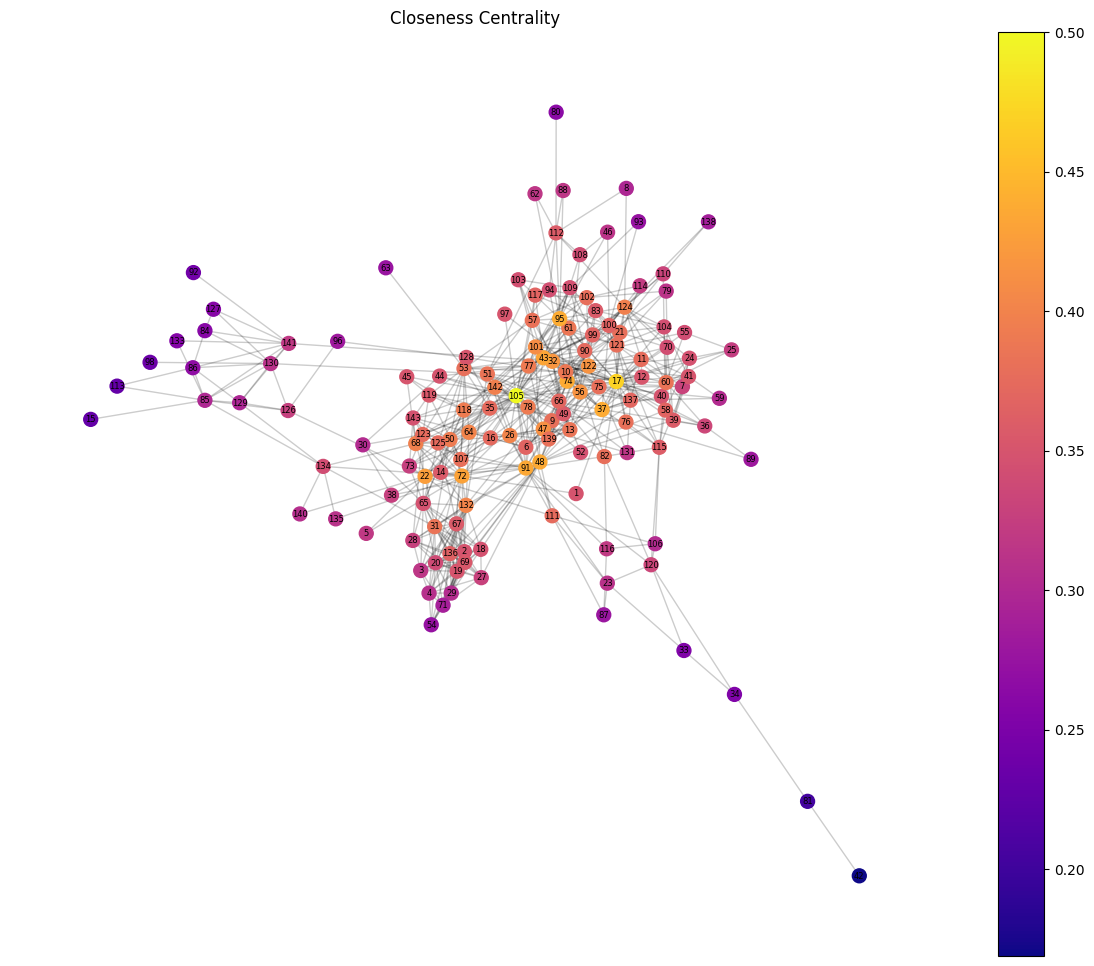

Analyzing the centrality measures of the Enron email network reveals key insights into the most influential nodes:

1. Degree Centrality

2. Betweenness Centrality

3. Closeness Centrality

Summary of Findings

6. Directed Network and PageRank Analysis

After analyzing the undirected network, we now consider the directionality of email exchanges by constructing a directed graph. This allows us to capture who sends and who receives emails, adding a new layer of insight into the communication dynamics.

D = nx.from_pandas_edgelist(data, source="sender", target="receiver", create_using=nx.DiGraph)
print(D)
DiGraph with 143 nodes and 623 edges
draw_graph(D, "Directed Network of Email Interactions")

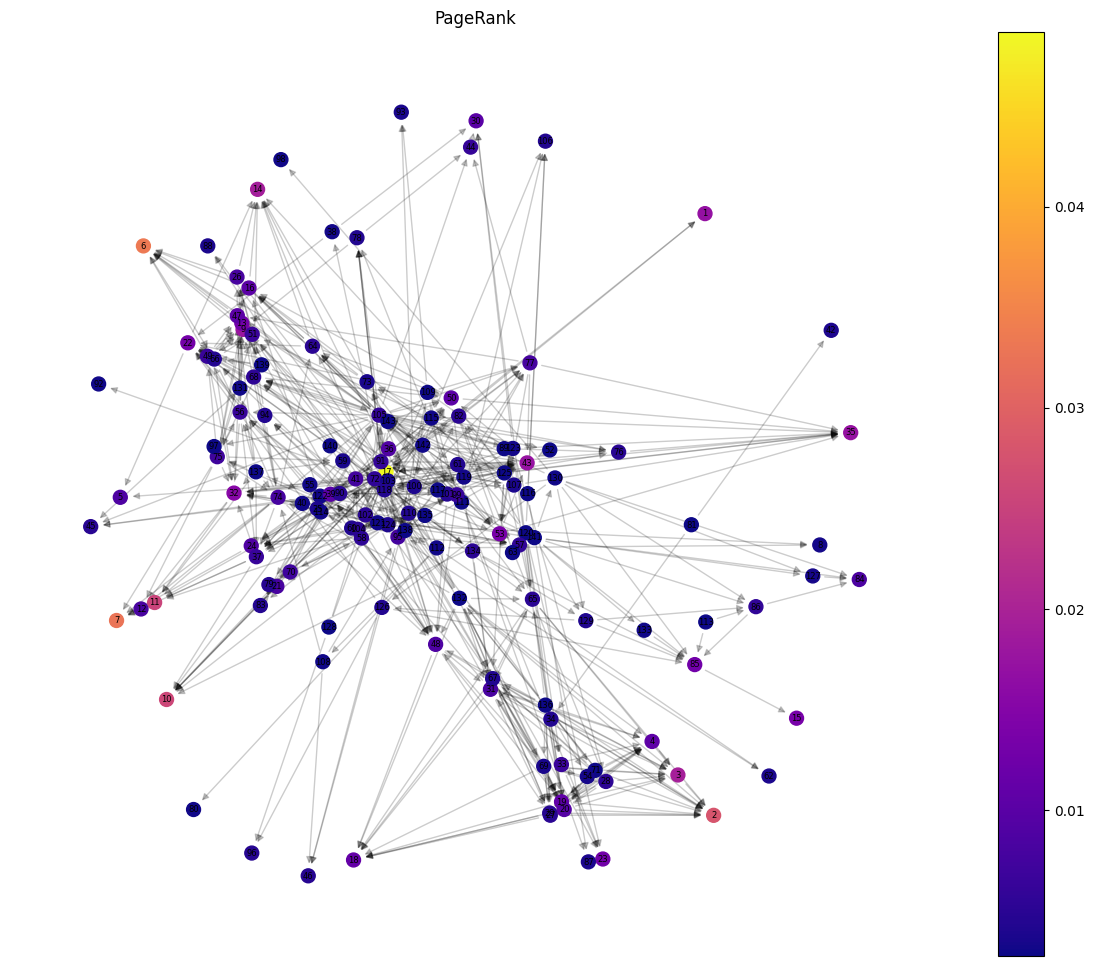
Nice, having our directed graph (DiGraph) built, we’ll now observe the PageRank of the nodes to understand their influence within the flow of communication. Unlike the undirected graph, this analysis takes into account the direction of email exchanges, highlighting not just who is connected but also how information flows across the network.

pr = nx.pagerank(D)
draw_centrality_graph(D, nx.pagerank(D), "PageRank")

The highest PageRank score is assigned to node 17, making it the most influential node in the network. This node acts as the primary hub, receiving emails from other significant nodes and ensuring the effective flow of communication.

7. Conslusions

a. Total Employees and Email Interactions

b. Maximum and Minimum Degree

c. Network Diameter

d. Average Shortest Path Length

e. Network Robustness

f. Most Important Nodes Based on Centrality

g. Most Important Node Based on PageRank

Final Conclusion

The Enron email network demonstrates a highly connected and efficient communication structure, with nodes 105 and 17 as its central figures. Node 105 dominates the undirected analysis due to its high connectivity, while node 17 leads in the directed graph, highlighting its influence in the flow of information. Despite its resilience to random failures, the network’s reliance on critical nodes and edges presents vulnerabilities under targeted attacks. This analysis underscores the importance of key players and the need to address vulnerabilities to ensure robust organizational communication systems.

Contact

Feel free to reach out through my social media.